The Background

Ecuador, a culturally rich country in Latin America, is home to Cuarenta - a traditional card game named after the Spanish word for 40. Though its origins are unclear, possibly rooted in colonial games, it remains popular, especially in Quito, where it is played during the annual Quito Festivities commemorating the city’s founding.

The story of Agent Dory began a few months ago, while sharing the game with friends in Canada. They had never heard of Cuarenta, but quickly took to it - enjoying the gameplay and devising strategies as they learned.

This experience made me rediscover the game with a different perspective. While games like poker and blackjack have been rigorously studied, regional games like Cuarenta often go unexplored.

It made me wonder - despite its long history, there may still be hidden patterns, strategies, or mechanics that have not been formalized. Perhaps certain elements of the game are so intuitive or culturally embedded that they have never been formally analyzed.

While the game is deeply interwoven with Ecuadorian identity - complete with colloquial sayings and humor - there’s untapped potential in exploring its technical aspects. It might even offer new insights for reinforcement learning agents and human intuition.

The Environment

The first step in building a proof-of-concept for Cuarenta was creating an environment-essentially a digital space where agents can live, learn, and play. Designed from scratch, this environment handles the core logic of the game: enforcing rules, managing points, and simulating mechanics.

At its core, the environment is made up of a deck and a table. The table is the central hub—it holds the players, keeps track of the cards in play, and manages key metrics throughout each round.

What makes the environment especially important is how it acts as both manager and interface. It processes game states and actions, serving as the translator between players and the game itself. For reinforcement learning agents, this kind of structure is essential.

The Player

With the environment in place, the next step was testing it with a player. The first player type was a simple one: a human player. This version interacts with the environment, to figure out the cards in hand, the scores and allows a human player to make a choice.

The Encoder

Enviroment Observations

With the environment in place, the player is able to interact with the environment using the iterface methods in table. However, an AI agent requires an understanding of the Enviroment. Observations are snapshots of the table that capture all the data from the perspective of the current player.

The observations are stored in a buffer. The data and strucuture of the observation is as follows:

The ObservationEncoder is responsible for transofmring the observations for better manipulation and normalization. All card related observations are one-hot encoded, that is an array of size 10 - A to 7, J, Q, K - has values from 0 to 1. If the hand has an A, the first element of the array added 0.25.

This is done for the current player’s hand, the cards on the table, and the seen cards.

Moreover, both teams’ scores are normalized - carton also over 40 -. Finally, the deck ratio is encoded along with the last card played.

The final strucutre looks like:

The Agent

After the environment was tested, the first agent was built on top of the human player rl_player. Since the interface and most methods were already defined, the only major difference was decision-making—which, in this case, had to be learned.

Designing the Architecture

The Learning Algorithm

There are many ways to train an agent—some are policy-based, others value-based. Each approach has its strengths. Actor-Critic methods offer a hybrid, leveraging the best of both worlds.

This agent uses Advantage Actor-Critic (A2C), which has two key components:

1. Actor – Decides which card to play based on the current policy
2. Critic – Evaluates how good the current state is (i.e., how promising the situation looks)

Both heads are have the following network structure:

The Actor maximizes the expected returns by adjusting a policy:

The advantage $A_{t} = R_{t} - CV{t}$, where $R_{t}$ are the rewards after taking an action - selecting a card - and $CV_{t}$ are the critic values.

And the Critic minimizes the MSE between the predicted value $CV_{t}$ and the return $R_{N}$:

At the end, both losses compose the A2C loss function:

The Memory Twist

This is where things get interesting.

Some games are fully observable—everyone sees everything. But Cuarenta isn’t like that. You only see your five cards, and by the time all the cards are revealed, the decisions that matter have already been made.

In other words, Cuarenta is a partially observable game. That changes everything.

To make good decisions, an agent has to remember key information—like which cards have already been played (there are only four of each rank). This makes memory a central requirement in the agent’s design.

It might be tempting to go with a Transformer model—after all, they’re the backbone of large language models and are great at assigning attention. But Transformers tend to struggle in Partially Observable Markov Decision Processes (POMDPs), particularly their struggle with modelling regular languages [1].

Research suggests that LRU memory models can work well in these cases [1,2]. But since support for LRU is still limited in standard libraries such as PyTorch, I opted for something more practical: an LSTM

The twist? An LSTM layer sits between the game state and both heads. This lets the agent “think” over time—learning patterns across rounds, recalling played cards, and planning for long-term consequences.

Before feeding the information to the LSTM, the observations are passed through a Feature Network and Strategy network.

The forward data flow is as follows:

The Move Data Flow

The logits from the actor represent a unnormalized log probabilities of selecting a card. Since there are at most 5 cards in hand at a time for each player, the invalid posibilities are masked to -inf.

In either case, the result is the value of the card to take from the current hand.

1
    def move(self, obs: np.ndarray, training: bool = True) -> int:
14 collapsed lines
2
        obs_tensor = torch.FloatTensor(obs).unsqueeze(
3
            0).unsqueeze(0)
4

5
        with torch.no_grad():
6
            action_logits, value, self.current_hidden = self.network(
7
                obs_tensor, self.current_hidden)
8

9
        action_dim = self.network.action_dim  # should be 10
10
        hand_set = set(self._hand)
11

12
        valid_mask = torch.tensor(
13
            [(v+1) in hand_set for v in range(action_dim)], dtype=torch.bool)
14
        masked_logits = action_logits.clone()
15
        masked_logits[0, ~valid_mask] = float('-inf')
16

17
        if self.training:
18
            dist = torch.distributions.Categorical(logits=masked_logits)
19
            card_value_idx = dist.sample().item()
20
        else:
21
            card_value_idx = torch.argmax(masked_logits, dim=-1).item()
22

23
        card_value = card_value_idx + 1
24
        self._hand.remove(card_value)
25
        return card_value

With all these elements, the dataflow for every move for every player is the following:

The Trainer

The model is trained by playing a loop of games against different models, being random player the base model. After every match, the final score that considers all the transitions of the player, and the outcome are stored as an episode_results.

The data is updated following the equations mentioned:

The data flow loosk like:

The Results

Training reinforcement learning agents in a game like Cuarenta is computationally intensive. While LSTMs help mitigate the risk, issues like vanishing gradients still require attention. Despite this, the current model shows promising performance—achieving an average win rate of around 70% against most agents, though curiously, the win rate is slightly lower against a random player. This suggests that the unpredictability of random actions may occasionally confuse the strategy.

Empirical analysis reveals that the agent picks up useful patterns over time, but it sometimes misses more complex plays—particularly those requiring short-term sacrifice for long-term gain. This points to a need for a more nuanced reward system that values long-term planning.

While the current model is just a first step, it highlights the exciting potential of applying reinforcement learning to partially observable environments. Future improvements might include:

• Experimenting with LRU architectures or Transformers to explore their effectiveness in this domain
• Designing more robust reward mechanisms
• Enhancing computational efficiency
• Introducing LLMs support

Even with room for growth, the current agent already offers a compelling challenge for the average human player—strategic, engaging, and surprisingly fun.

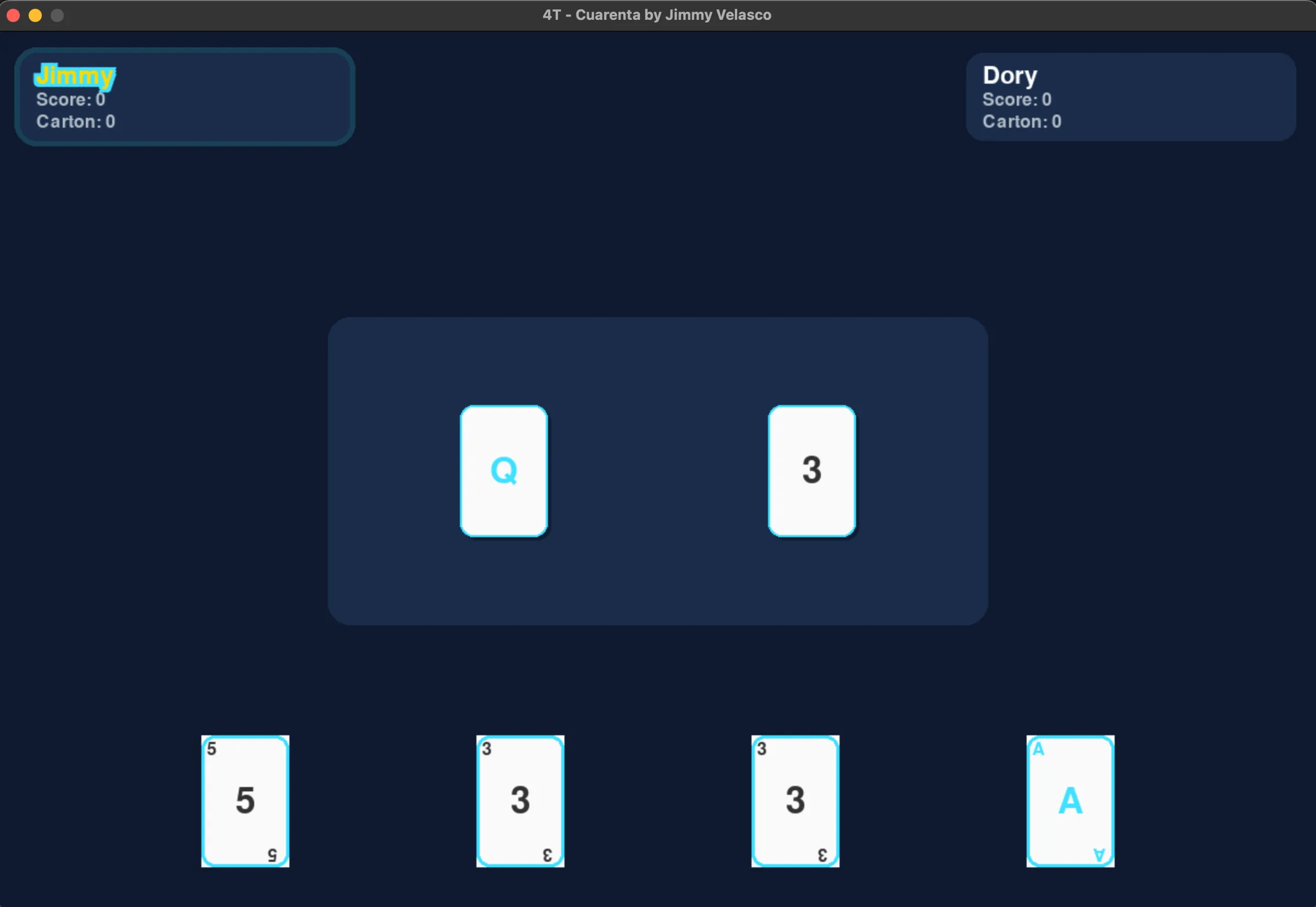
The Fun

To support the human aspect of the game. A GUI was created using PyGame. This allows the users to drag and drop cards on the table, see the both scoring systems (points and carton) and Have a clearer understanding of the rounds. The rules of the game are described below. I would highly encourage to give the game a try and ideally grab a deck of cards and enjoy a traditional game.

References

[1] A. Gupta, A. Jomaa, F. Locatello, and G. Martius, “Structured World Models for Planning and Exploration,” arXiv preprint arXiv:2405.17358, May 2024. [Online]. Available: https://arxiv.org/pdf/2405.17358

[2] R. Orvieto, A. Kirsch, A. Gupta, S. Lacoste-Julien, A. Krause, and S. W. Linderman, “Resurrecting the sigmoid in deep learning through dynamical isometry: theory and practice,” in Proceedings of the 40th International Conference on Machine Learning (ICML), vol. 202, 2023, pp. 27054–27086. [Online]. Available: https://proceedings.mlr.press/v202/orvieto23a/orvieto23a.pdf

[3] L. Tunstall, “Understanding deep reinforcement learning with A2C,” Hugging Face Blog, Jul. 2022. [Online]. Available: https://huggingface.co/blog/deep-rl-a2c

The Rules

Overview

Cuarenta is played between two teams, each with one or two players. The goal is simple: reach 40 points before the opposing team.

A standard 52-card French deck is used, but cards with rank 8, 9, and 10 are removed. These are instead used to keep score during the game.

Each team sits opposite each other so turns alternate between teams. The deck is made up of 40 playable cards, with card values determined by their rank (Aces are 1; J, Q, K have no numeric value).

Dealing and Rounds

Each player receives 5 cards per round, dealt clockwise from the player to the left of the dealer. Once all cards are played, a new 5-card hand is dealt. This continues until all 40 cards are used.

At the end of each full deck cycle, scores are tallied, cards are reshuffled, and the dealer rotates. The cycle repeats until a team reaches 40 points.

Scoring Mechanics

There are multiple ways to earn points during the game:

Caída

Occurs when a player places a card, and the next player plays the same rank immediately after. This awards 2 points to the team making the second move.

Cartón

Collected cards (via various mechanics) are stored in a pile called the cartón. Cartón points are awarded at the end of each 40-card cycle based on how many cards a team holds.

• First 19 cards: No points
• Starting from the 20th card: score begins at 6
• Each additional card increases the score by 1
• The total is rounded up to the next even number Example: 23 cards → Start counting at 6 → Ends at 9 → Rounded up to 10 points

Limpia

If a play results in clearing all cards from the table, it’s called a limpia and grants 2 points. If the limpia also happens through a caída, it gives 4 points total (2 for caída, 2 for limpia).

Ways to Capture Cards

Pairs

If a card on the table matches the rank of the card played, it can be collected. If this happens directly after another player places the same rank, it also counts as a caída.

Sequences

If there are consecutive cards on the table (e.g., 2, 3, 4) and a player plays a card that starts the sequence (e.g., 2), the player collects the full sequence starting from that rank. Sequence order: A, 2, 3, 4, 5, 6, 7, J, Q, K

Sums

If the sum of two or more cards on the table equals the card being played, they can all be collected.

Chained Mechanics

Sum and sequence mechanics can be combined. Example: Table: 3, 2, 6, 7 → Player plays 5 3 + 2 = 5 (valid sum) → Also starts sequence 5, 6, 7 → Collects all 6 cards.

Special Rules

Ronda

If a player is dealt three cards of the same rank, their team earns 2 points. The rank is hidden unless it’s revealed by a caída, in which case the opposing team earns 10 points and the round restarts.

Mesa

If a player is dealt four cards of the same rank, their team wins the game instantly.

30-Point Rule

Once a team reaches 30 points, cartón points no longer count. They must reach 40 through caída, ronda, or limpia.

38-Point Rule

At 38 points, only caída can earn the remaining 2 points needed to win.

Keeping Score with Real Cards

The removed 8s, 9s, and 10s are used to keep score physically:

• A card face-up = 2 points
• A card face-down = 10 points

For instance, five face-up cards = 10 points → Trade for one face-down card. This system provides a visual and practical way to track points during play.